BCA TU, Math II – Unit 5: Differential Equations

Differential equations are equations that involve an unknown function and its derivatives. They are essential in modeling growth, decay, motion, population, economics, and many physical systems.

1. Definition of Differential Equation

A differential equation (DE) relates a function with its derivatives.

Example:

Here, is the unknown function of .

2. Order and Degree of a Differential Equation

• Order: Highest derivative present.
• Degree: Power of the highest derivative (if the DE is polynomial in derivatives).

Example:

• Order = 2 (highest derivative is )
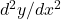• Degree = 3 (highest derivative raised to power 3)

3. First Order, First Degree Differential Equations

Can be written as:

General solution involves one arbitrary constant.

4. Differential Equations with Separable Variables

If the DE can be written as:

Then, separate variables:

Example:

→

5. Homogeneous Differential Equations

A first-order DE is homogeneous if:

Substitution: →

Example:

Put :

So,

6. Exact Differential Equations

A DE of the form:

is exact if:

Solution: There exists a function such that:

Example:

Check:

Integrate w.r.t :

Differentiate w.r.t :

Final Solution:

Key Takeaways

1. Order: Highest derivative; Degree: Power of highest derivative.
2. First-order DEs include separable, homogeneous, and exact equations.
3. Separable: Separate 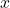and 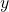, integrate both sides.
4. Homogeneous: Use substitution .
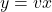5. Exact: Check condition .
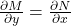6. Solutions always include arbitrary constants, representing families of curves.