BCA TU, Math II – Unit 6: Computational methods

Computational methods are numerical techniques used to solve mathematical problems that may not have exact solutions or are too complex for analytical methods. These techniques are widely applied in computer science, engineering, economics, and applied mathematics.

1. Linear Programming Problem (LPP)

LPP is a method to maximize or minimize a linear objective function subject to linear constraints.

General Form:

$\text{Maximize (or Minimize)} ; Z = c_1 x_1 + c_2 x_2 + \dots + c_n x_n$

Subject to constraints:

$a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n \le b_1, \quad x_i \ge 0$

Applications: resource allocation, production planning, transport scheduling.

(i) Graphical Solution (for 2 variables)

Plot the constraints on a graph.
Find the feasible region.
Evaluate the objective function 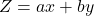$Z = ax + by$ at corner points.
Maximum/minimum value lies at a corner point.

2. Solution of LPP by Simplex Method (up to 3 variables)

Used when there are more than 2 variables.

Steps:

Convert inequalities to equalities (introduce slack variables).
Set up the initial simplex tableau.
Iteratively pivot to improve objective function.
Stop when no further improvement is possible.

3. Solution of System of Linear Equations

(i) Gauss Elimination Method

Converts the system into upper triangular form, then applies back substitution.

Example:

$2x + y = 5, \quad 4x - 6y = -2$ → Solution: $x = 1, ; y = 3$

(ii) Gauss-Seidel Method

Iterative method: start with initial guesses, update repeatedly until convergence.
Often used for large systems.

(iii) Matrix Inversion Method

For $AX = B$ , solution is:

$X = A^{-1} B$

Where $A^{-1}$ is the inverse of the coefficient matrix.

4. Solving Non-Linear Equations

(i) Bisection Method

Root-finding method that repeatedly divides an interval in half.
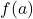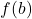If $f(a)$ and $f(b)$ have opposite signs, a root lies in $[a,b]$ .

Midpoint formula:

$c = \frac{a+b}{2}$

(ii) Newton-Raphson Method

Faster root-finding method.
Formula:

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

Requires derivative and a good initial approximation.

Example: Find $\sqrt{2}$ using $f(x) = x^2 - 2$

Start $x_0 = 1$ :

$x_1 = 1 - \frac{1^2 - 2}{2(1)} = 1.5, \quad x_2 = 1.4167, \dots$

Applications

Engineering: stress analysis, electrical circuits.
Computer Science: optimization, scheduling.
Economics: cost minimization, profit maximization.
Science: solving complex models in physics and chemistry.

Key Takeaways

LPP deals with optimization under constraints: graphical (2 variables) and simplex (≥3 variables).
Gauss elimination → direct method; Gauss-Seidel → iterative method.
Matrix inversion gives exact solutions when inverse exists.
Bisection method → simple, always convergent, but slower.
Newton-Raphson method → fast, requires derivative and good initial guess.
Computational methods are essential for large-scale real-world problems without exact algebraic solutions.

Menu

BCA TU, Math II – Unit 6: Computational methods