Integration is the reverse process of differentiation. While differentiation deals with the rate of change, integration deals with accumulation — such as finding area under curves, total distance, volume, and surface area.
1. Riemann Integral
The Riemann integral defines integration as the limit of sums of areas of rectangles under a curve.
If a function ![]() is continuous on
is continuous on ![]() , then:
, then:
![]()
where ![]() .
.
2. Fundamental Theorem of Calculus (Without Proof)
Connects differentiation and integration:
If ![]() is an antiderivative of
is an antiderivative of ![]() , then:
, then:
![]()
Differentiation and integration are inverse processes.
3. Techniques of Integration
Basic Rules
![]()
![]()
Standard Integrals
![]()
![]()
![]()
![]()
![]()
Substitution Method
If ![]() , then:
, then:
![]()
Integration by Parts
![]()
Partial Fractions
Used for rational functions.
4. Definite and Improper Integrals
- Definite Integral:
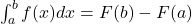
- Improper Integrals: Extend to infinity or discontinuous functions.
Example:
![]()
5. Applications of Definite Integrals
- Area under Curve:
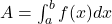
- Length of Arc (Rectification):
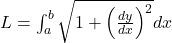
- Volume of Solid of Revolution:
Rotating curve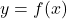 around x-axis:
around x-axis: ![Rendered by QuickLaTeX.com V = \pi \int_a^b [f(x)]^2 dx](https://bcaguidenepal.com/wp-content/ql-cache/quicklatex.com-b750e5658a899611dac4a6cedbb0a6b3_l3.png)
- Surface Area of Revolution:
![]()
6. Numerical Integration
Used when exact integration is difficult:
Trapezoidal Rule
![]()
Simpson’s Rule
![]()
7. Worked Examples
- Find:
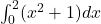
![]()
Area under curve ![]() from 0 to 1:
from 0 to 1:
![]()
Volume of solid when ![]() , from 0 to 4, rotated around x-axis:
, from 0 to 4, rotated around x-axis:
![]()
Key Takeaways
- Integration is the reverse of differentiation → used to accumulate quantities.
- Fundamental theorem links definite integrals to antiderivatives.
- Techniques include: substitution, integration by parts, and partial fractions.
- Applications: area, volume, arc length, and surface area.
- Numerical methods (Trapezoidal & Simpson’s rule) approximate integrals.
- Improper integrals extend integration to infinity or discontinuities.




