February 2, 2026

BCA Guide Nepal

Ultimate guide to BCA TU

BCA TU, Math II – Unit 2: Differentiation

admin06 mins

Differentiation is one of the core concepts of calculus. It studies how a function changes as its input changes. In simple terms, the derivative represents the rate of change or the slope of a curve at any point.

1. Ordered Pairs and Cartesian Product

  • Ordered Pair (a, b): A pair of numbers where the order matters.
  • Cartesian Product: If A = {1,2}, ; B = {x,y}, then

A \times B = {(1,x), (1,y), (2,x), (2,y)}

This idea is the basis for plotting functions on the coordinate plane.

2. Relation, Domain, and Range

  • Relation: A set of ordered pairs (x, y)
  • Domain: Set of all possible input values (x)
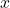  • Range: Set of all possible output values (y)

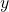Example:
For f(x) = \sqrt{x},

  • Domain: x \ge 0
  • Range: y \ge 0

3. Functions

A function is a special type of relation where each input has exactly one output.

  • Notation: f: X \to Y, \quad f(x) = y

Example: f(x) = x^2

Inverse Function:
If f(x) : a \to b, then f^{-1}(x) : b \to a

Example:
If f(x) = 2x + 3, then f^{-1}(x) = \frac{x-3}{2}

4. Special Types of Functions

  • Identity Function: f(x) = x
  • Constant Function: f(x) = c (horizontal line)

Algebraic Functions:

  • Linear: f(x) = ax + b → straight line
  • Quadratic: f(x) = ax^2 + bx + c → parabola
  • Cubic: f(x) = ax^3 + bx^2 + cx + d → S-shaped curve

Trigonometric Functions:
f(x) = \sin x, \cos x, \tan x → periodic, wave-like graphs

Exponential Function:
f(x) = a^x, ; a>0, a \neq 1 → rapid growth or decay
Example: f(x) = 2^x

Logarithmic Function:
f(x) = \log_a x, ; a>0, a \neq 1 → inverse of exponential
Example: f(x) = \ln x

5. Composite Function

A composite function is formed when one function is applied after another:

(f \circ g)(x) = f(g(x))

Example:
If f(x) = x^2, g(x) = x + 1, then

(f \circ g)(x) = f(g(x)) = (x+1)^2

6. Differentiation – The Core Idea

The derivative of f(x) with respect to x is:

f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}

  • Represents the slope of the tangent line to the curve at point x
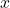
  • Represents the instantaneous rate of change

Example 1:

f(x) = x^2 \quad \Rightarrow \quad f'(x) = 2x

Example 2:

f(x) = \sin x \quad \Rightarrow \quad f'(x) = \cos x

7. Rules of Differentiation

  • Power Rule: \frac{d}{dx}(x^n) = n x^{n-1}
  • Sum Rule: \frac{d}{dx}[f(x) + g(x)] = f'(x) + g'(x)
  • Product Rule: ' = u'v + uv'
  • Quotient Rule: \left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2}
  • Chain Rule: ' = f'(g(x)) \cdot g'(x)

8. Worked Problems

  1. Differentiate: y = 3x^3 - 2x^2 + 5x - 1

y' = 9x^2 - 4x + 5

Differentiate: y = \sin(2x)
Using chain rule: y' = 2\cos(2x)

Differentiate: y = \frac{x^2 + 1}{x}
Using quotient rule: y' = \frac{(2x)(x) - (x^2 + 1)(1)}{x^2} = \frac{x^2 - 1}{x^2}

Key Takeaways

  • A function relates each input to one output; its domain and range must be clear.
  • Special functions include algebraic, trigonometric, exponential, and logarithmic functions.
  • Composite functions involve applying one function to another.
  • Differentiation measures rate of change and slope of curves.
  • Important rules: power, product, quotient, chain.
  • Applications include curve sketching, optimization, and solving real-world problems.

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Related