Calculus begins with the fundamental concepts of limits and continuity. These ideas help us understand how functions behave near certain points and whether they flow smoothly without breaks.
1. Limit of a Function
- The limit of a function describes the value the function approaches as the input approaches some number.
- Definition:
Meaning: as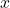
gets very close to 
, 
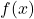gets very close to 
. - Example 1:
Example 2 (Non-direct substitution):
2. Indeterminate Forms
Some limits cannot be evaluated directly and produce forms like:
, 
, 
, 
, 
, 
, 
These require algebraic manipulation or special techniques (e.g., L’Hôpital’s Rule).
- Example:
3. Algebraic Properties of Limits (without proof)
If
and 
, then:
- Sum:
![\lim_{x \to a} [f(x) + g(x)] = L + M](https://bcaguidenepal.com/wp-content/ql-cache/quicklatex.com-e29632824e70a70c5782c6197e1e05c9_l3.png "Rendered by QuickLaTeX.com")
- Difference:
![\lim_{x \to a} [f(x) - g(x)] = L - M](https://bcaguidenepal.com/wp-content/ql-cache/quicklatex.com-b8ade2321860920e9723eda55434d144_l3.png "Rendered by QuickLaTeX.com")
- Product:
![\lim_{x \to a} [f(x) \cdot g(x)] = L \cdot M](https://bcaguidenepal.com/wp-content/ql-cache/quicklatex.com-467e319a61e8454e42789f1f97df9229_l3.png "Rendered by QuickLaTeX.com")
- Quotient:
- Constant Multiple:
![\lim_{x \to a} [c \cdot f(x)] = c \cdot L](https://bcaguidenepal.com/wp-content/ql-cache/quicklatex.com-637023c5475713bd33a05444e401c210_l3.png "Rendered by QuickLaTeX.com")
, where 
is a constant.
4. Theorems on Limits of Functions
- Algebraic Functions: Direct substitution works if the denominator is non-zero.
- Transcendental Functions: (Exponential, trigonometric, logarithmic) often need special results.
- Examples:
5. Continuity of a Function
A function is continuous at 
if:
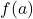exists
exists
If any condition fails, the function is discontinuous at
Graphical idea: A continuous function can be drawn without lifting the pen.
6. Types of Discontinuity
- Removable: Hole in the graph (limit exists but function not defined).
- Example:
- Example:
- Jump: Sudden jump in value.
- Example: Step functions.
- Infinite: Function goes to infinity near the point.
- Example:
- Example:
7. Exercises (Illustrative Problems)
- Evaluate:
Solution:
- Test continuity at
:
- Left limit:
- Right limit:
- Function value:
Function is continuous at 0.
Key Takeaways
- Limits define the value a function approaches as input nears a point.
- Indeterminate forms require algebraic manipulation.
- Properties of limits help in solving complex problems step by step.
- A function is continuous if its value matches the limit at a point.
- Discontinuities can be removable, jump, or infinite.
- Mastery of limits and continuity is essential before moving into differentiation.
